什么是深度优先搜索和广度优先搜索

如果T是G的一个生成子图而且又是一棵树，则称T是图G的一棵生成树（spanning tree）或支撑树。

生成树T中的边称为树T的树枝（branch）,不在生成树T中的G的边，称为树T的弦（chord）

定理1：图G有生成树G为连通图。

深度优先搜索：

求连通简单图G的一棵生成树的许多方法中，深度优先搜索（depth first search）是一个十分重要的算法。

基本思想：

任意选择图G的一个顶点v0作为根，通过相继地添加边来形成在顶点v0开始的路，其中每条新边都与路上的最后一个顶点以及不在路上的一个顶点相关联。继续尽可能多地添加边到这条路。若这条路经过图G的所有顶点，则这条路即为G的一棵生成树；若这条路没有经过G的所有顶点，不妨设形成这条路的顶点顺序v0,v1,......,vn。则返回到路里的次最后顶点v(n-1).若有可能，则形成在顶点v(n-1)开始的经过的还没有放过的顶点的路；否则，返回到路里的顶点v(n-2)。然后再试。重复这个过程，在所访问过的最后一个顶点开始，在路上次返回的顶点，只要有可能就形成新的路，知道不能添加更多的边为止。

深度优先搜索也称为回溯（back tracking）

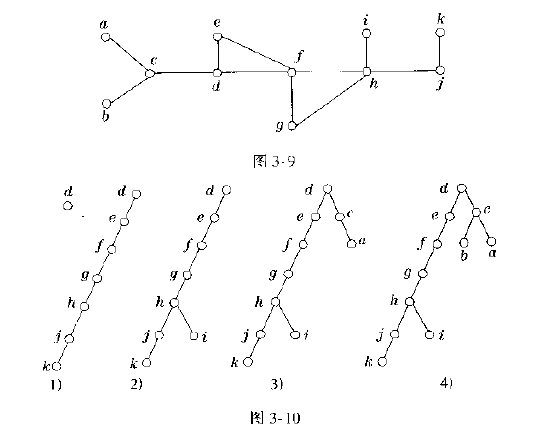
用深度优先搜哦所来找出图3-9所示图G的生成树，任意地从顶点d开始，生成步骤显示在图3-10。

广度优先搜索：

可用广度优先搜索（breadth first search）来产生连通简单图的生成树。

基本思想：

从图的顶点中任意第选择一个根，然后添加与这个顶点相关联的所有边，在这个阶段添加的新顶点成为生成树里1层上的顶点，任意地排序它们。下一步，按照顺序访问1层上的每一个顶点，只要不产生回路，就添加与这个顶点相关联的每个边。这样就产生了树里2的上的顶点。遵循同样的原则继续下去，经有限步骤就产生了生成树。

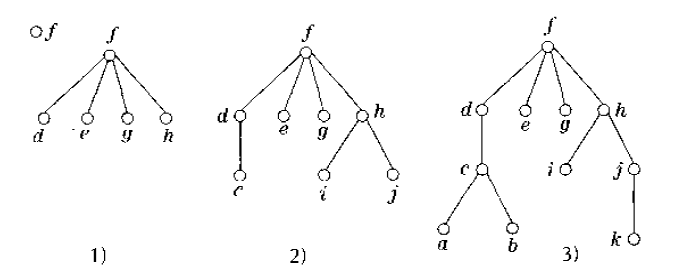
用广度优先搜索找出图3-9所示图G的生成树，选择顶点f作为根。